Whenever you conduct a hypothesis test, you will get a test statistic as a result. To determine if the results of the hypothesis test are statistically significant, you can compare the test statistic to a Z critical value. If the absolute value of the test statistic is greater than the Z critical value, then the results of the test are statistically significant.
To find the Z critical value on a TI-84 calculator, we can use the following function:
invNorm(probability, μ, σ)
where:
- probability: the significance level
- μ: population mean
- σ: population standard deviation
You can access this function on a TI-84 calculator by pressing 2nd and then pressing vars. This will take you to a DISTR screen where you can then use invNorm():
This tutorial shares several examples of how to use the invNorm() function to find Z critical values on a TI-84 calculator.
Example 1: Z Critical Value for a Left-Tailed Test
Question: Find the Z critical value for a left-tailed test with a significance level of 0.05.
Answer: invNorm(.05, 0, 1) = -1.6449
Interpretation: If the test statistic of the test is less than -1.6449, then the results of the test are statistically significant at α = 0.05.
Example 2: Z Critical Value for a Right-Tailed Test
Question: Find the Z critical value for a right-tailed test with a significance level of 0.10.
Answer: invT(1-.10, 0, 1) = 1.2816
Interpretation: If the test statistic of the test is greater than 1.2816, then the results of the test are statistically significant at α = 0.10.
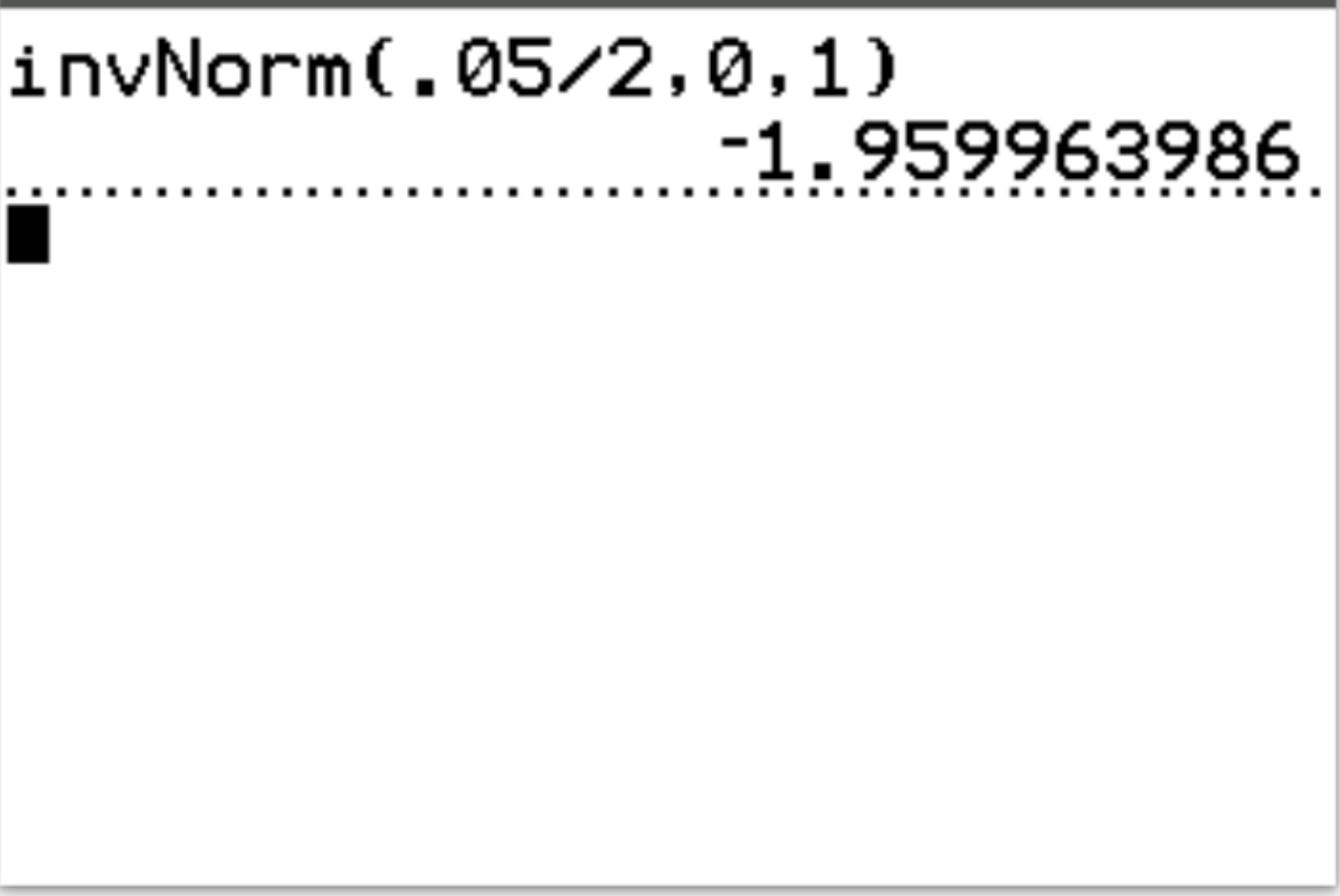
Example 3: Z Critical Value for a Two-Tailed Test
Question: Find the Z critical value for a two-tailed test with a significance level of 0.05.
Answer: invNorm(.05/2, 0, 1) = -1.96, 1.96
Interpretation: Since this is a two-tailed test, we actually have two critical values: -1.96 and 1.96. If the test statistic of the test is less than -1.96 or greater than 1.96, then the results of the test are statistically significant at α = 0.05.