How to Calculate Quartiles for Grouped Data

Quartiles are values that split up a dataset into four equal parts.

You can use the following formula to calculate quartiles for grouped data:

Q_i = L + (C/F) * (iN/4 – M)

where:

• L: The lower bound of the interval that contains the i^th quartile
• C: The class width
• F: The frequency of the interval that contains the i^th quartile
• N: The total frequency
• M: The cumulative frequency leading up to the interval that contains the i^th quartile

The following example shows how to use this formula in practice.

Example: Calculate Quartiles for Grouped Data

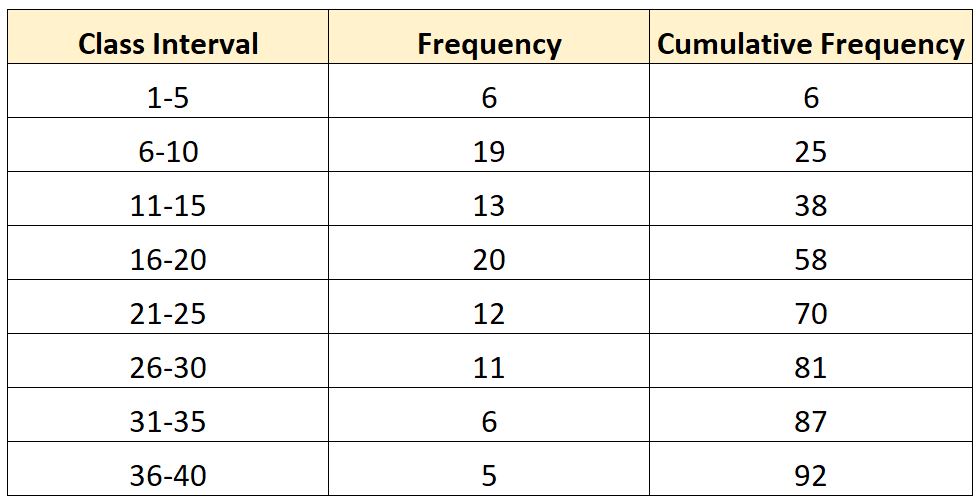
Suppose we have the following frequency distribution:

Now suppose we’d like to calculate the value at the third quartile (Q₃) of this distribution.

The value at the third quartile will be located at position (iN/4) in the distribution.

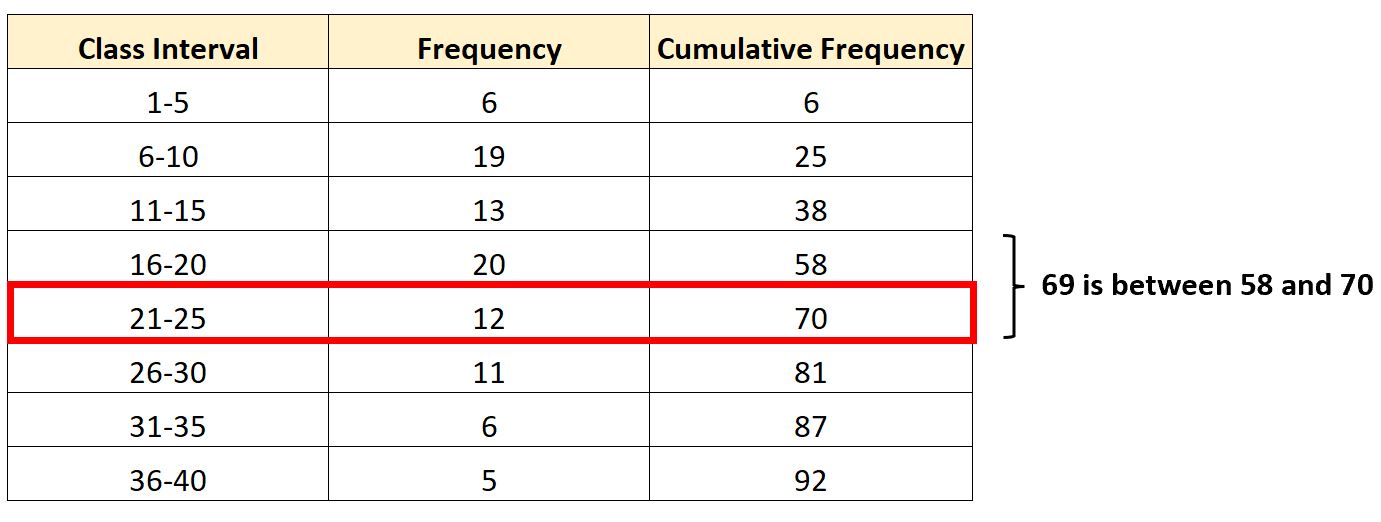
Thus, (iN/4) = (3*92/4) = 69.

The interval that contains the third quartile will be the 21-25 interval since 69 is between the cumulative frequencies of 58 and 70.

Knowing this, we can find each of the values necessary to plug into our formula:

L: The lower bound of the interval that contains the i^th quartile

• The lower bound of the interval is 21.

C: The class width

• The class width is calculated as 25 – 21 = 4.

F: The frequency of the interval that contains the i^th quartile

• The frequency of the 21-25 class is 12

N: The total frequency

• The total cumulative frequency in the table is 92.

M: The cumulative frequency leading up to the interval that contains the i^th quartile

• The cumulative frequency leading up to the 21-25 class is 58.

We can then plug in all of these values into the formula from earlier to find the value at the third quartile:

• Q_i = L + (C/F) * (iN/4 – M)
• Q₃ = 21 + (4/12) * ((3)(92)/4 – 58)
• Q₃ = 24.67

The value at the third quartile is 24.67.

You can use a similar approach to calculate the values for the first and second quartiles.

Additional Resources

The following tutorials provide additional information for working with grouped data:

How to Find Mean & Standard Deviation of Grouped Data
How to Find the Mode of Grouped Data
How to Find the Median of Grouped Data
Grouped vs. Ungrouped Frequency Distributions