Nonresponse bias is the bias that occurs when the people who respond to a survey differ significantly from the people who do not respond to the survey.
Nonresponse bias can occur for several reasons:
- The survey is poorly designed and leads to nonresponses. For example, excessively long surveys without incentives may cause a large percentage of people to not complete the survey.
- Certain people are more likely to respond to a particular survey. For example, people who go rock climbing often are more likely to respond to a survey about a potential new rock climbing facility than people who don’t go rock climbing.
- The survey didn’t reach all members of a population. For example, a survey sent out on a new phone app may only reach younger people who have the app, which leads to nonresponses from older members of the population.
- The survey asks embarrassing questions about private information that make many people unwilling to respond.
Nonresponse bias can occur for all of these reasons.
Why is Nonresponse Bias a Problem?
Nonresponse bias is a problem for two main reasons:
1. Nonresponse bias causes the sample to be unrepresentative of the population as a whole. The whole point of collecting data for a sample is that it’s quicker and cheaper than collecting data for an entire population, and to be able to extrapolate the findings from the sample to the larger population.
In order to extrapolate the findings, though, the sample needs to be representative of our population as a whole. Ideally we would like our sample to be a “mini” version of the population.
Unfortunately, nonresponse bias can cause the people in our sample to be significantly different than the people in the larger population.
For example, suppose a city is considering building a new rock climbing facility. To gauge how interested people in the city would be in using this type of facility, city officials send out a short survey via a new smartphone app.
Because of the method used to deliver the survey and because of the content on the survey (rock climbing questions), mostly young people who have the app and who are interested in rock climbing respond.
Thus, when the survey results come back it appears that an overwhelming majority of people in the city are interested in having this new facility built. Unfortunately, the results from the survey are not representative of the larger population.
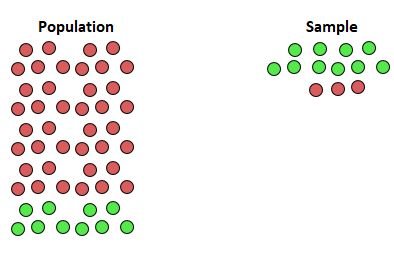
The visual below illustrates this problem: suppose the green circles represent people who are interested in using the facility while the red circles represent people who are not interested in using the facility:
Notice how the sample is not representative of the larger population. The results of the survey would show that most people are excited about a new rock climbing facility. Unfortunately, if city officials assumed that this sample was representative of the population, they may decide to build the facility and then quickly realize that far fewer people would use it than they thought.
2. Nonresponse bias can cause larger variance for estimates. If the sample size of the survey turns out to be smaller than the sample size researchers had planned to use, the variance for the estimates of the study may be larger than planned.
For example, from hypothesis testing we know that the larger our sample size, the lower the variance on our estimate for a population mean or a population proportion. However, the smaller our sample size, the higher the variance on our estimates for population parameters, and the harder it is to find a statistically significant finding.
Examples of Nonresponse Bias
The following examples illustrate several cases in which nonresponse bias can occur.
Example 1
Researchers want to know how computer scientists perceive a new software program. There is pressure to get as much data as possible from the survey, so the researchers design a survey that takes roughly one hour to complete. When they distribute the survey, they find that many computer scientists either don’t respond at all or begin to respond but eventually quit before completing the entire survey.
When researchers get the data back, they find that the respondents perceive the software to be excellent and high quality. However, once they roll out the new software to the entire population of computer scientists they find that they receive mostly negative feedback.
It turns out that the people who took the time to complete the entire survey turned out to be mostly entry-level computer scientists who were unable to assess the flaws of the program.
Because of this, respondents of the survey did not reflect the larger computer scientist population as whole and thus the results of the survey were unreliable.
Example 2
Researchers want to learn about alcohol consumption rates at a certain college. They decide to set up a booth on campus where students can stop and take a questionnaire in regards to how much and how often they consume alcohol. Unfortunately, the questionnaire is not anonymous so only students who drink very little or not at all choose to fill out the questionnaire.
When the results come back, it appears that alcohol consumption is low and infrequent among students. Unfortunately, the respondents of the survey are not reflective of the larger population of students on campus and thus the findings are unreliable.
Example 3
One classic example of nonresponse bias is the 1936 Presidential Election. A popular publication at the time ran a poll that predicted Alf Landon would beat Franklin D. Roosevelt by a landslide. However, when the election took place Franklin D. Roosevelt actually won by a landslide.
It turns out that of the 10 million questionnaires sent out, only 2.3 million people responded. The 7.7 million who did not respond turned out to be significantly different in terms of political preference.
Thus, the results of the questionnaire were not reflective of the population as a whole, which is why the prediction that Alf Landon would win turned out to be so incorrect.
How to Prevent Nonresponse Bias
Nonresponse bias can be prevented (or at least mitigated) by taking the following steps:
- Design the survey to be relatively short. The longer a survey, the less likely people are to take time out of their day to respond.
- Offer incentives for completing the survey. Incentives generally increase response rates.
- Make sure that people know answers to the survey will be confidential or anonymous. This generally makes people more willing to respond.
- Distribute the survey in such a way that it reaches a large percentage of the population, e.g. use traditional forms of distribution rather than a new app that few people have.
While it’s not always possible to completely eliminate the effects of nonresponse bias, it’s possible to minimize the effects by using a smart survey design and distribution method.
Additional Resources
What is Self-Selection Bias?
What is Undercoverage Bias?
What is Referral Bias?