Simple linear regression is a statistical method you can use to quantify the relationship between a predictor variable and a response variable.
This tutorial explains how to perform simple linear regression by hand.
Example: Simple Linear Regression by Hand
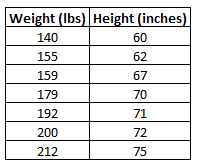
Suppose we have the following dataset that shows the weight and height of seven individuals:
Use the following steps to fit a linear regression model to this dataset, using weight as the predictor variable and height as the response variable.
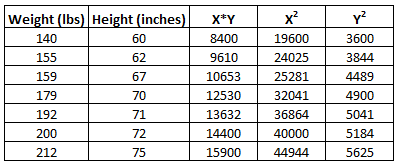
Step 1: Calculate X*Y, X2, and Y2
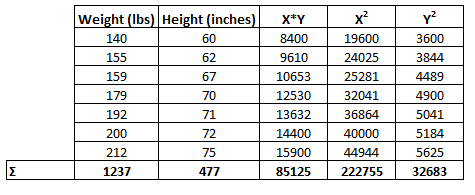
Step 2: Calculate ΣX, ΣY, ΣX*Y, ΣX2, and ΣY2
Step 3: Calculate b0
The formula to calculate b0 is: [(ΣY)(ΣX2) – (ΣX)(ΣXY)] / [n(ΣX2) – (ΣX)2]
In this example, b0 = [(477)(222755) – (1237)(85125)] / [7(222755) – (1237)2] = 32.783
Step 4: Calculate b1
The formula to calculate b1 is: [n(ΣXY) – (ΣX)(ΣY)] / [n(ΣX2) – (ΣX)2]
In this example, b1 = [7(85125) – (1237)(477)] / [7(222755) – (1237)2] = 0.2001
Step 5: Place b0 and b1 in the estimated linear regression equation.
The estimated linear regression equation is: ŷ = b0 + b1*x
In our example, it is ŷ = 0.32783 + (0.2001)*x
How to Interpret a Simple Linear Regression Equation
Here is how to interpret this estimated linear regression equation: ŷ = 32.783 + 0.2001x
b0 = 32.7830. When weight is zero pounds, the predicted height is 32.783 inches. Sometimes the value for b0 can be useful to know, but in this example it doesn’t actually make sense to interpret b0 since a person can’t weigh zero pounds.
b1 = 0.2001. A one pound increase in weight is associated with a 0.2001 inch increase in height.
Simple Linear Regression Calculator
We can double check our results by inputting our data into the simple linear regression calculator:
This equation matches the one that we calculated by hand.