The term inverse normal distribution refers to the method of using a known probability to find the corresponding z-critical value in a normal distribution.
This is not to be confused with the Inverse Gaussian distribution, which is a continuous probability distribution.
This tutorial provides several examples of how to use the inverse normal distribution in different statistical softwares.
Inverse Normal Distribution on a TI-83 or TI-84 Calculator
You’re most likely to encounter the term “inverse normal distribution” on a TI-83 or TI-84 calculator, which uses the following function to find the z-critical value that corresponds to a certain probability:
invNorm(probability, μ, σ)
where:
- probability: the significance level
- μ: population mean
- σ: population standard deviation
You can access this function on a TI-84 calculator by pressing 2nd and then pressing vars. This will take you to a DISTR screen where you can then use invNorm():
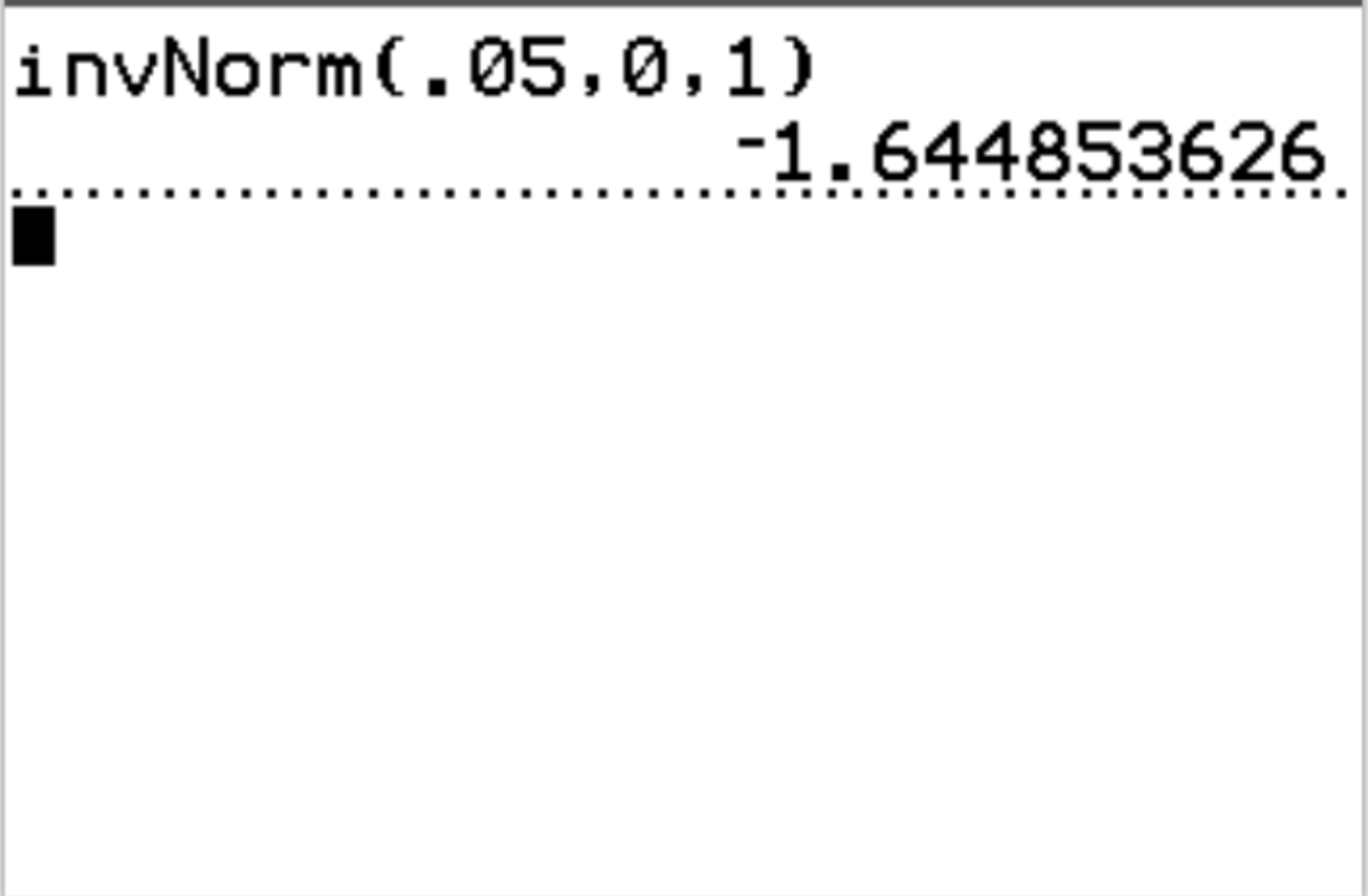
For example, we can use this function to find the z-critical value that corresponds to a probability value of 0.05:
The z-critical value that corresponds to a probability value of 0.05 is -1.64485.
Related: How to Use invNorm on a TI-84 Calculator (With Examples)
Inverse Normal Distribution in Excel
To find the z-critical value associated with a certain probability value in Excel, we can use the INVNORM() function, which uses the following syntax:
INVNORM(p, mean, sd)
where:
- p: the significance level
- mean: population mean
- sd: population standard deviation
For example, we can use this function to find the z-critical value that corresponds to a probability value of 0.05:
The z-critical value that corresponds to a probability value of 0.05 is -1.64485.
Inverse Normal Distribution in R
To find the z-critical value associated with a certain probability value in R, we can use the qnorm() function, which uses the following syntax:
qnorm(p, mean, sd)
where:
- p: the significance level
- mean: population mean
- sd: population standard deviation
For example, we can use this function to find the z-critical value that corresponds to a probability value of 0.05:
qnorm(p=.05, mean=0, sd=1) [1] -1.644854
Once again, the z-critical value that corresponds to a probability value of 0.05 is -1.64485.