The binomial distribution table is a table that shows probabilities associated with the binomial distribution. To use the binomial distribution table, you only need three values:
- n: the number of trials
- r: the number of “successes” during n trials
- p: the probability of success on a given trial
Using these three numbers, you can use the binomial distribution table to find the probability of obtaining exactly r successes during n trials when the probability of success on each trial is p.
The following examples illustrate how to read the binomial distribution table.
Example 1
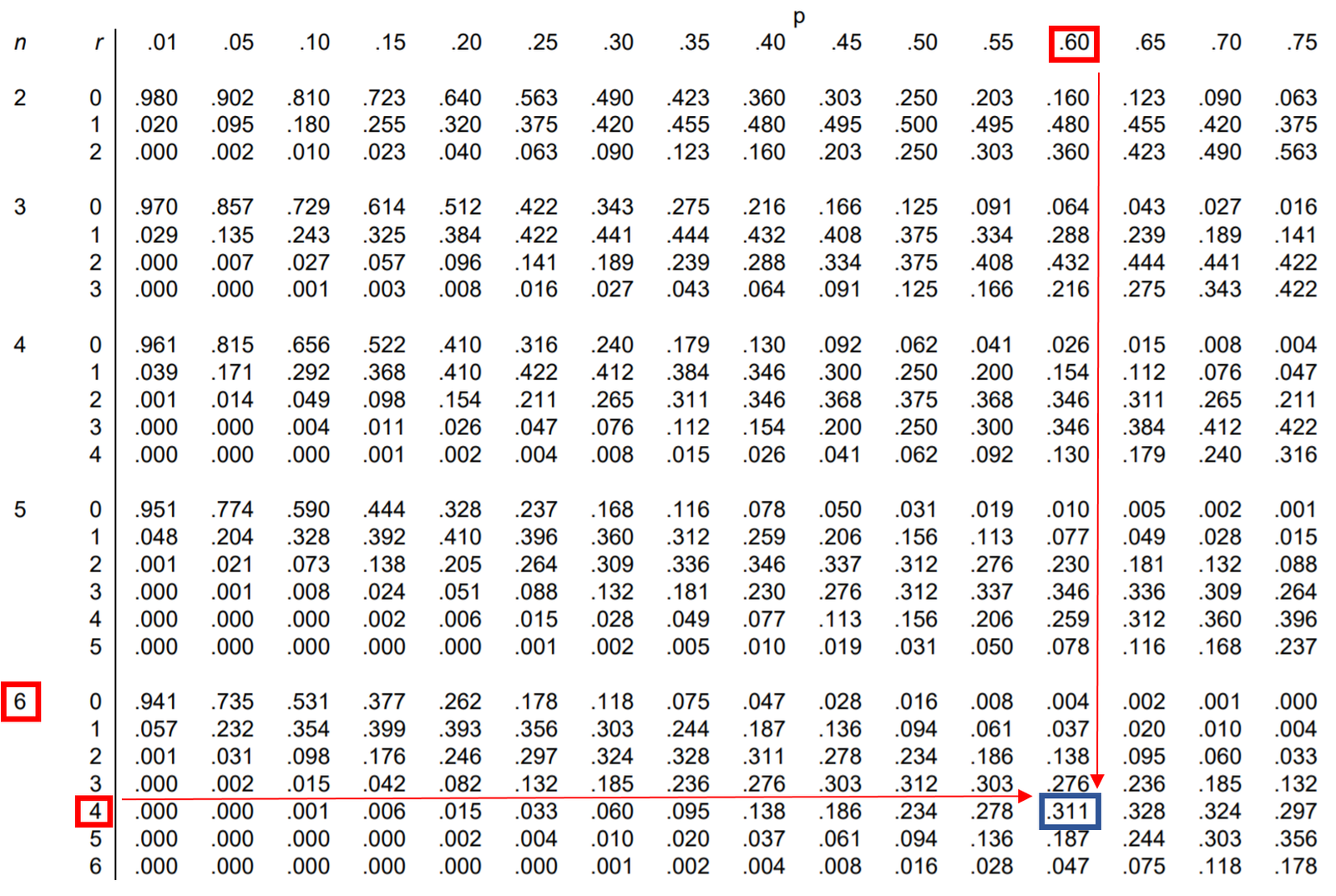
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes exactly 4?
To answer this question, we can look up the value in the binomial distribution table that corresponds to n = 6, r = 4, and p = 0.60:
The probability that Jessica makes exactly 4 out of 6 free throws is 0.311.
Example 2
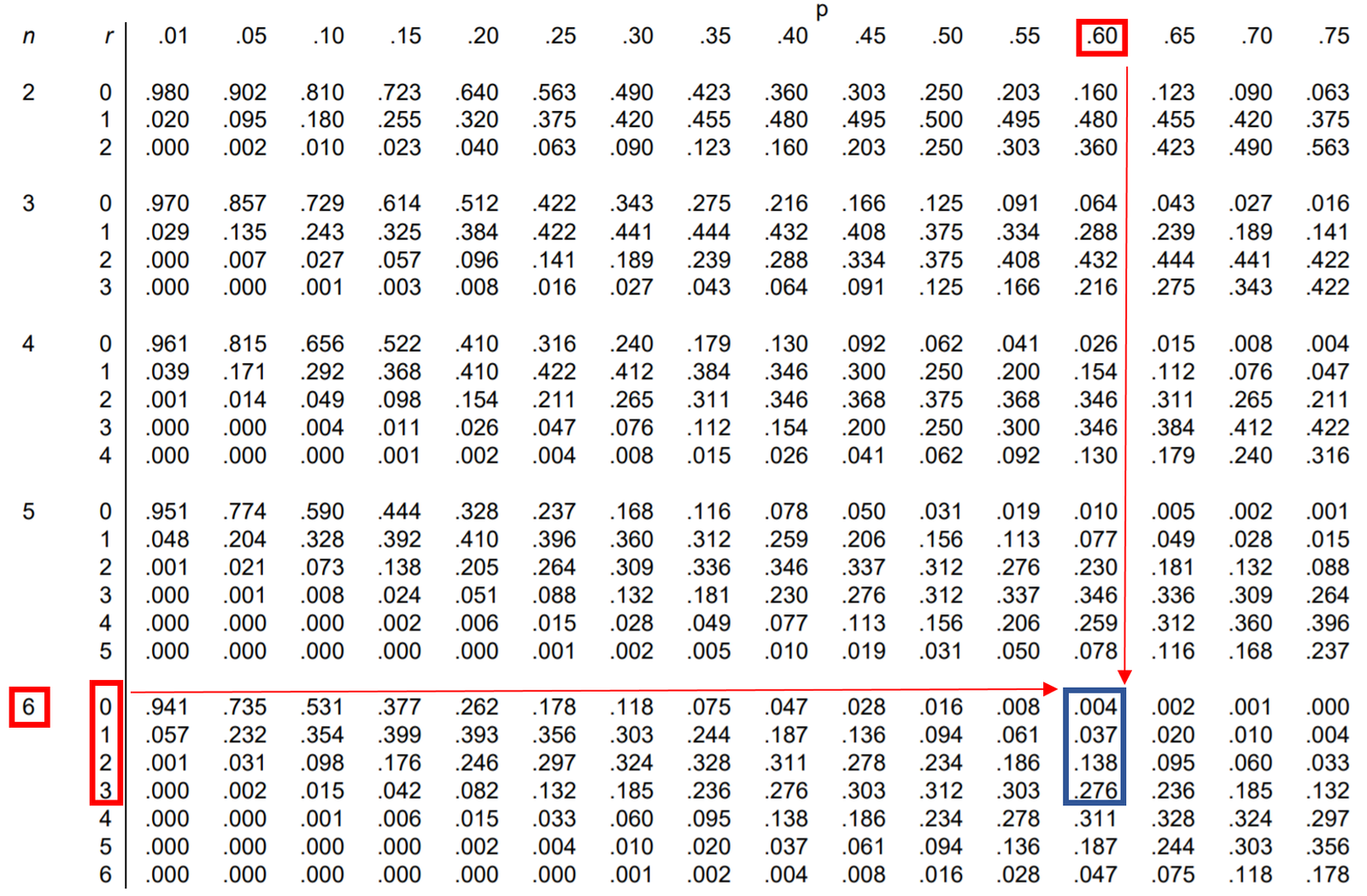
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes less than 4?
To find this probability, we actually have to add up the following probabilities:
P(makes less than 4) = P(makes 0) + P(makes 1) + P(makes 2) + P(makes 3)
So, we can look up each of these four probabilities in the binomial distribution table and add them up:
According to the table, P(makes less than 4) = .004 + .037 + .138 + .276 = 0.455.
The probability that Jessica makes less than 4 free throws is 0.455.
Example 3
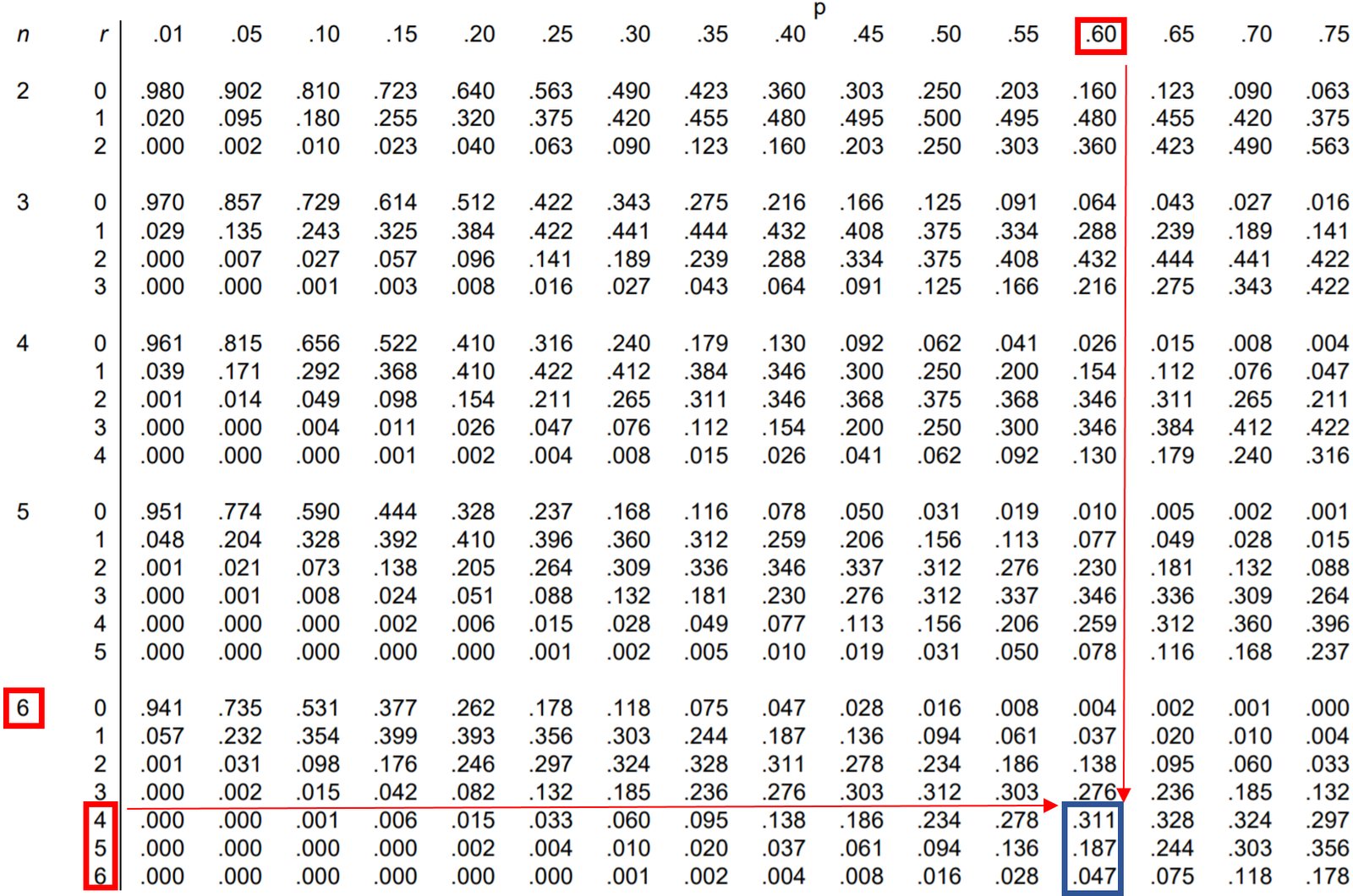
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes 4 or more?
To find this probability, we have to add up the following probabilities:
P(makes 4 or more) = P(makes 4) + P(makes 5) + P(makes 6)
So, we can look up each of these three probabilities in the binomial distribution table and add them up:
According to the table, P(makes 4 or more) = .311 + .187 + .047 = 0.545.
The probability that Jessica makes 4 or more free throws is 0.545.