A confidence interval is a range of values that is likely to contain a population parameter with a certain level of confidence. It is calculated using the following general formula:
Confidence Interval = (point estimate) +/- (critical value)*(standard error)
This formula creates an interval with a lower bound and an upper bound, which likely contains a population parameter with a certain level of confidence:
Confidence Interval = [lower bound, upper bound]
This tutorial explains how to calculate the following confidence intervals in Excel:
1. Confidence Interval for a Mean
2. Confidence Interval for a Difference in Means
3. Confidence Interval for a Proportion
4. Confidence Interval for a Difference in Proportions
Let’s jump in!
Example 1: Confidence Interval for a Mean
We use the following formula to calculate a confidence interval for a mean:
Confidence Interval = x +/- z*(s/√n)
where:
- x: sample mean
- z: the chosen z-value
- s: sample standard deviation
- n: sample size
Example: Suppose we collect a random sample of turtles with the following information:
- Sample size n = 25
- Sample mean weight x = 300
- Sample standard deviation s = 18.5
The following screenshot shows how to calculate a 95% confidence interval for the true population mean weight of turtles:
The 95% confidence interval for the true population mean weight of turtles is [292.75, 307.25].
Example 2: Confidence Interval for a Difference in Means
We use the following formula to calculate a confidence interval for a difference in population means:
Confidence interval = (x1–x2) +/- t*√((sp2/n1) + (sp2/n2))
where:
- x1, x2: sample 1 mean, sample 2 mean
- t: the t-critical value based on the confidence level and (n1+n2-2) degrees of freedom
- sp2: pooled variance, calculated as ((n1-1)s12 + (n2-1)s22) / (n1+n2-2)
- t: the t-critical value
- n1, n2: sample 1 size, sample 2 size
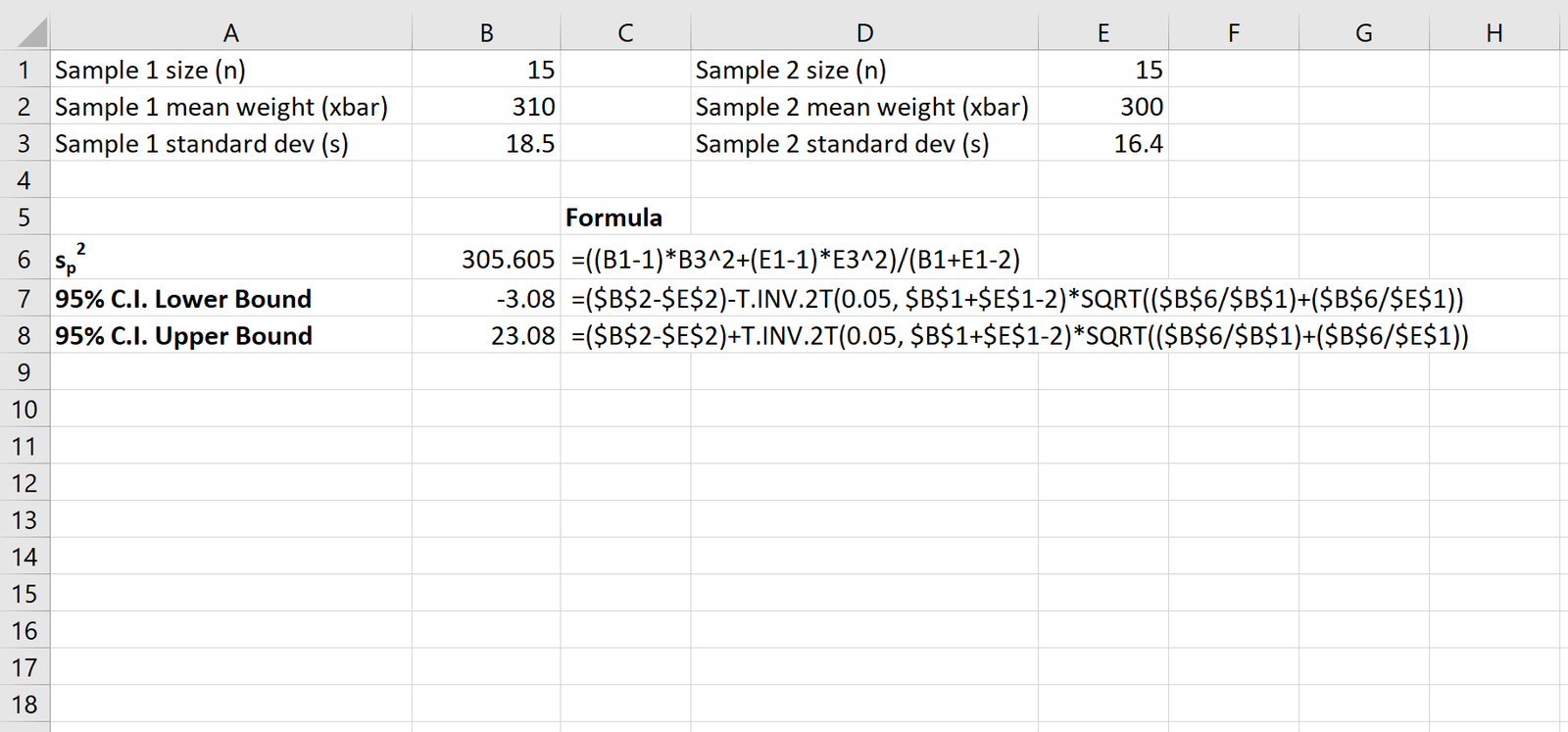
Example: Suppose we want to estimate the difference in mean weight between two different species of turtles, so we go out and gather a random sample of 15 turtles from each population. Here is the summary data for each sample:
Sample 1:
- x1 = 310
- s1 = 18.5
- n1 = 15
Sample 2:
- x2 = 300
- s2 = 16.4
- n2 = 15
The following screenshot shows how to calculate a 95% confidence interval for the true difference in population means:
The 95% confidence interval for the true difference in population means is [-3.08, 23.08].
Example 3: Confidence Interval for a Proportion
We use the following formula to calculate a confidence interval for a proportion:
Confidence Interval = p +/- z*√p(1-p) / n
where:
- p: sample proportion
- z: the chosen z-value
- n: sample size
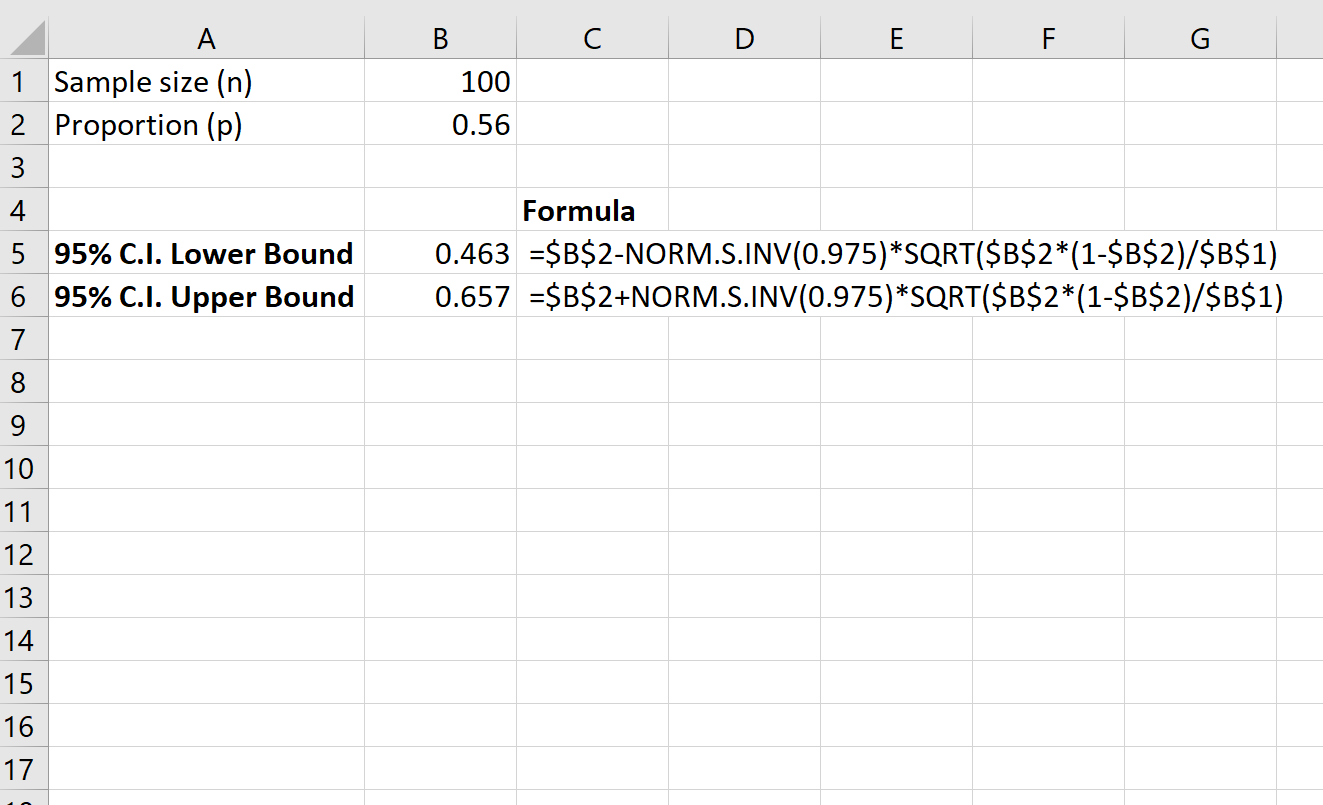
Example: Suppose we want to estimate the proportion of residents in a county that are in favor of a certain law. We select a random sample of 100 residents and ask them about their stance on the law. Here are the results:
- Sample size n = 100
- Proportion in favor of law p = 0.56
The following screenshot shows how to calculate a 95% confidence interval for the true proportion of residents in the entire county who are in favor of the law:
The 95% confidence interval for the true proportion of residents in the entire county who are in favor of the law is [.463, .657].
Example 4: Confidence Interval for a Difference in Proportions
We use the following formula to calculate a confidence interval for a difference in proportions:
Confidence interval = (p1–p2) +/- z*√(p1(1-p1)/n1 + p2(1-p2)/n2)
where:
- p1, p2: sample 1 proportion, sample 2 proportion
- z: the z-critical value based on the confidence level
- n1, n2: sample 1 size, sample 2 size
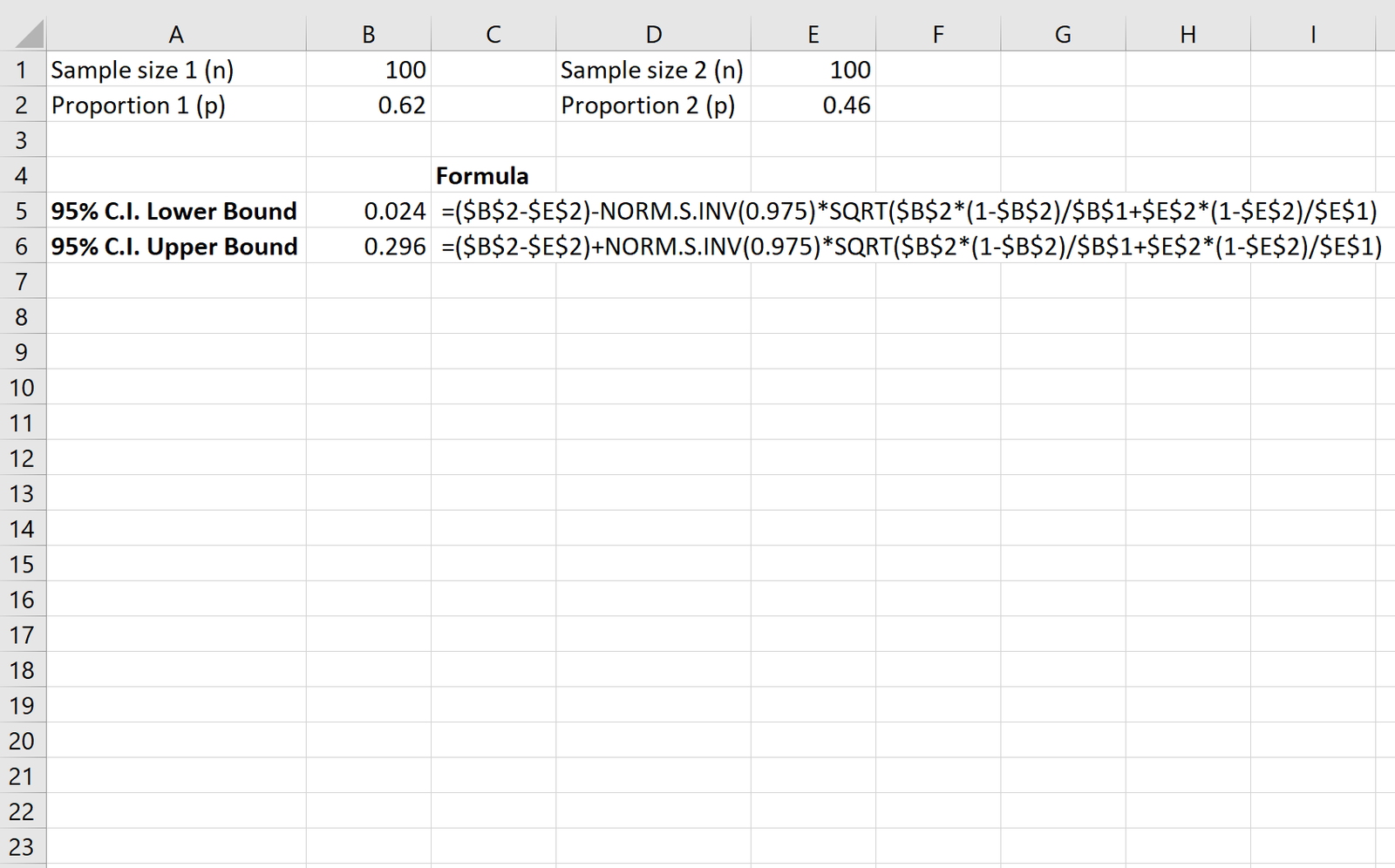
Example: Suppose we want to estimate the difference in the proportion of residents who support a certain law in county A compared to the proportion who support the law in county B. Here is the summary data for each sample:
Sample 1:
- n1 = 100
- p1 = 0.62 (i.e. 62 out of 100 residents support the law)
Sample 2:
- n2 = 100
- p2 = 0.46 (i.e. 46 our of 100 residents support the law)
The following screenshot shows how to calculate a 95% confidence interval for the true difference in proportion of residents who support the law between the counties:
The 95% confidence interval for the true difference in proportion of residents who support the law between the counties is [.024, .296].
You can find more Excel tutorials here.