Bayes’ Theorem states the following for any two events A and B:
P(A|B) = P(A)*P(B|A) / P(B)
where:
- P(A|B): The probability of event A, given event B has occurred.
- P(B|A): The probability of event B, given event A has occurred.
- P(A): The probability of event A.
- P(B): The probability of event B.
For example, suppose the probability of the weather being cloudy is 40%. Also suppose the probability of rain on a given day is 20% and that the probability of clouds on a rainy day is 85%.
If it’s cloudy outside on a given day, what is the probability that it will rain that day?
Solution:
- P(cloudy) = 0.40
- P(rain) = 0.20
- P(cloudy | rain) = 0.85
Thus, we can calculate:
- P(rain | cloudy) = P(rain) * P(cloudy | rain) / P(cloudy)
- P(rain | cloudy) = 0.20 * 0.85 / 0.40
- P(rain | cloudy) = 0.425
If it’s cloudy outside on a given day, the probability that it will rain that day is 0.425 or 42.5%.
The following example shows how to solve this exact problem using Bayes’ Theorem in Excel.
Example: Bayes’ Theorem in Excel
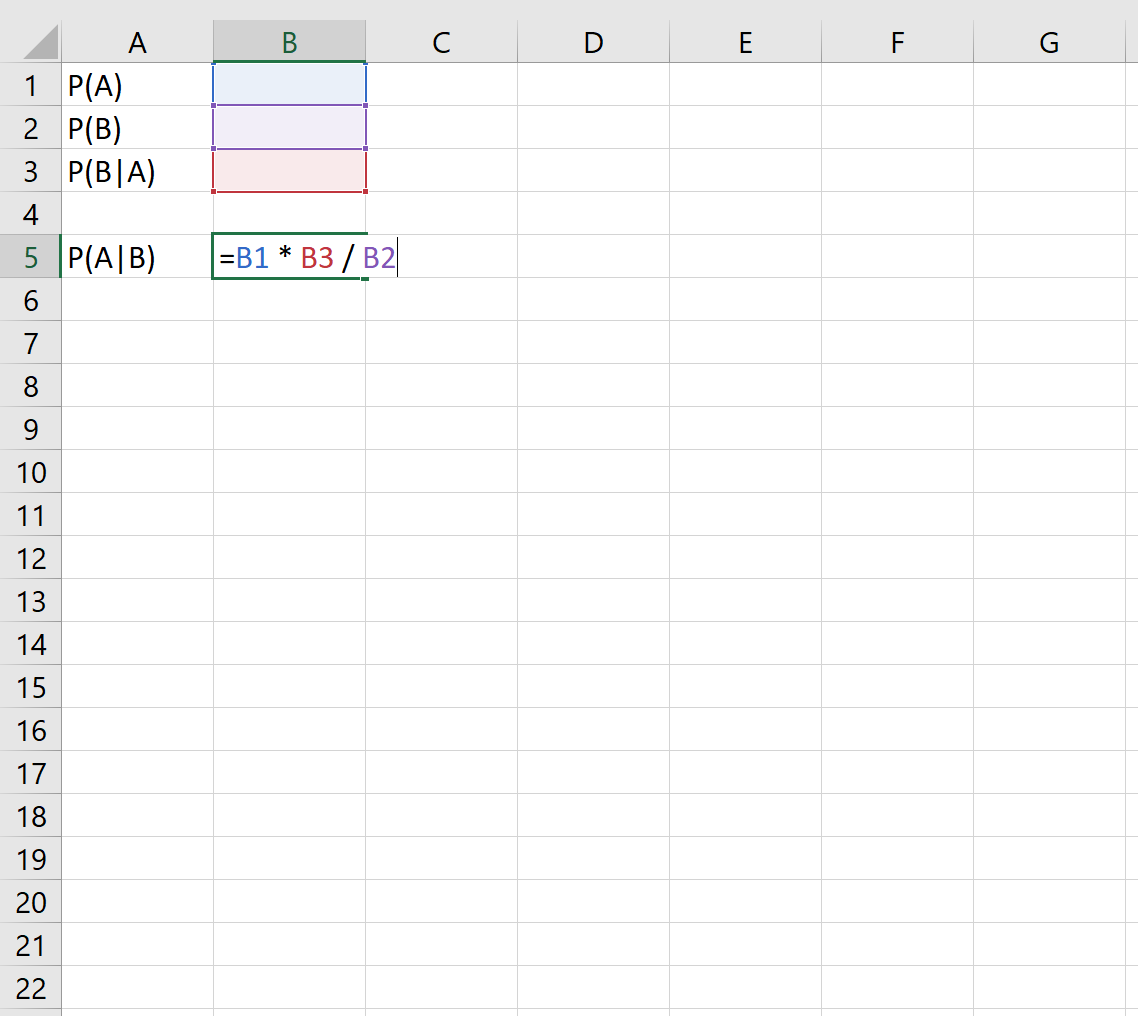
The following formula shows how to apply Bayes’ Theorem in Excel:
For example, if we know the following probabilities:
- P(cloudy) = 0.40
- P(rain) = 0.20
- P(cloudy | rain) = 0.85
Then we can simply plug these into the cells in Excel:
This tells us that if it’s cloudy outside on a given day, the probability that it will rain that day is 0.425 or 42.5%.
Additional Resources
How to Calculate Conditional Probability in Excel
How to Apply the Empirical Rule in Excel
How to Apply the Central Limit Theorem in Excel