How to Find Sample Variance on a TI-84 Calculator

The sample variance tells us how spread out the values are in a given sample.

Typically denoted as s², it is calculated as:

s² = Σ (x_i – x)² / (n-1)

where:

• x: sample mean
• x_i: the i^th value in the sample
• n: the sample size

The following step-by-step example shows how to calculate the sample variance for the following sample:

Sample: 2, 4, 4, 7, 8, 12, 14, 15, 19, 22

Step 1: Enter the Data

First, we will enter the data values.

Press Stat, then press EDIT. Then enter the values of the sample in column L1:

Step 2: Find the Sample Variance

Next, press Stat and then scroll over to the right and press CALC.

Then press 1-Var Stats.

In the new screen that appears, press Enter.

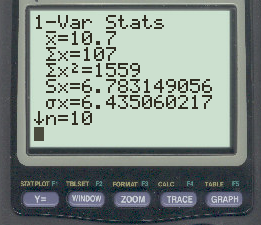
Once you press Enter, a list of summary statistics will appear.

The sample standard deviation is Sx = 6.783149056.

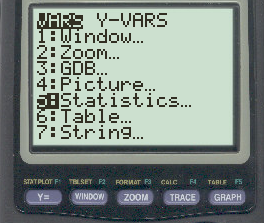
To find the sample variance, we need to square this value. To do so, press VARS and then press 5:

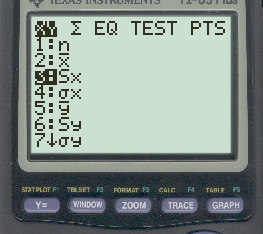
In the new window that appears, press 3 to select the sample standard deviation:

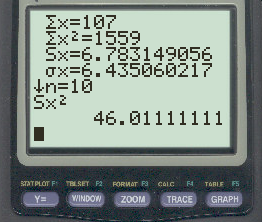
Lastly, press the x² button to square the sample standard deviation:

The sample variance turns out to be 46.0111.

Additional Resources

How to Find a Five Number Summary on a TI-84 Calculator
How to Find Interquartile Range on a TI-84 Calculator
How to Find Coefficient of Variation on a TI-84 Calculator