A studentized residual is simply a residual divided by its estimated standard deviation.
In practice, we typically say that any observation in a dataset that has a studentized residual greater than an absolute value of 3 is an outlier.
We can quickly obtain the studentized residuals of any regression model in R by using the studres() function from the MASS package, which uses the following syntax:
studres(model)
where model represents any linear model.
Example: Calculating Studentized Residuals in R
Suppose we build the following simple linear regression model in R, using the built-in mtcars dataset:
#build simple linear regression model
model
We can use the studres() function from the MASS package to calculate the studentized residuals for each observation in the dataset:
library(MASS)
#calculate studentized residuals
stud_resids #view first three studentized residuals
head(stud_resids, 3)
Mazda RX4 Mazda RX4 Wag Datsun 710
-0.6236250 -0.6236250 -0.7405315
We can also create a quick plot of the predictor variable values vs. the corresponding studentized residuals:
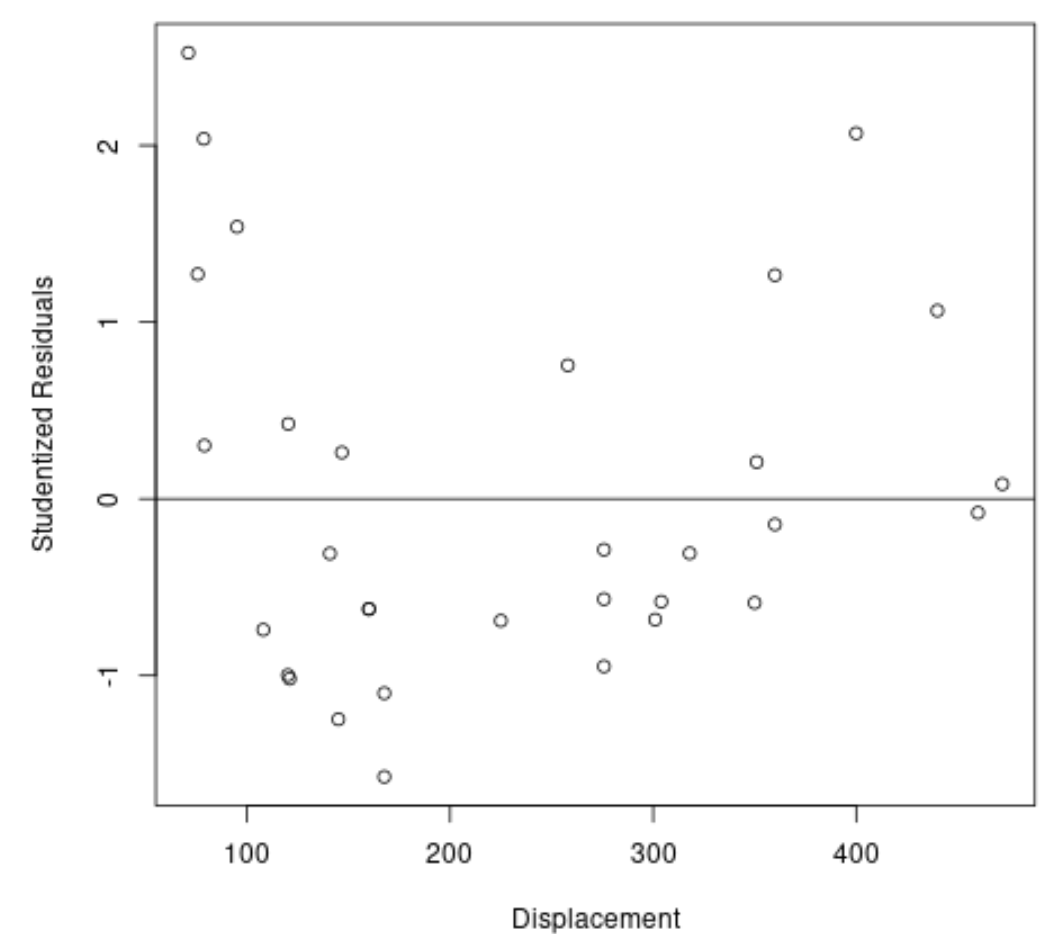
#plot predictor variable vs. studentized residuals plot(mtcars$disp, stud_resids, ylab='Studentized Residuals', xlab='Displacement') #add horizontal line at 0 abline(0, 0)
From the plot we can see that none of the observations have a studentized residual with an absolute value greater than 3, thus there are no clear outliers in the dataset.
We can also add the studentized residuals of each observation back into the original dataset if we’d like:
#add studentized residuals to orignal dataset final_data cbind(mtcars[c('mpg', 'disp')], stud_resids) #view final dataset head(final_data) mpg disp stud_resids Mazda RX4 21.0 160 -0.6236250 Mazda RX4 Wag 21.0 160 -0.6236250 Datsun 710 22.8 108 -0.7405315 Hornet 4 Drive 21.4 258 0.7556078 Hornet Sportabout 18.7 360 1.2658336 Valiant 18.1 225 -0.6896297
We can then sort each observation from largest to smallest according to its studentized residual to get an idea of which observations are closest to being outliers:
#sort studentized residuals descending final_data[order(-stud_resids),] mpg disp stud_resids Toyota Corolla 33.9 71.1 2.52397102 Pontiac Firebird 19.2 400.0 2.06825391 Fiat 128 32.4 78.7 2.03684699 Lotus Europa 30.4 95.1 1.53905536 Honda Civic 30.4 75.7 1.27099586 Hornet Sportabout 18.7 360.0 1.26583364 Chrysler Imperial 14.7 440.0 1.06486066 Hornet 4 Drive 21.4 258.0 0.75560776 Porsche 914-2 26.0 120.3 0.42424678 Fiat X1-9 27.3 79.0 0.30183728 Merc 240D 24.4 146.7 0.26235893 Ford Pantera L 15.8 351.0 0.20825609 Cadillac Fleetwood 10.4 472.0 0.08338531 Lincoln Continental 10.4 460.0 -0.07863385 Duster 360 14.3 360.0 -0.14476167 Merc 450SL 17.3 275.8 -0.28759769 Dodge Challenger 15.5 318.0 -0.30826585 Merc 230 22.8 140.8 -0.30945955 Merc 450SE 16.4 275.8 -0.56742476 AMC Javelin 15.2 304.0 -0.58138205 Camaro Z28 13.3 350.0 -0.58848471 Mazda RX4 Wag 21.0 160.0 -0.62362497 Mazda RX4 21.0 160.0 -0.62362497 Maserati Bora 15.0 301.0 -0.68315010 Valiant 18.1 225.0 -0.68962974 Datsun 710 22.8 108.0 -0.74053152 Merc 450SLC 15.2 275.8 -0.94814699 Toyota Corona 21.5 120.1 -0.99751166 Volvo 142E 21.4 121.0 -1.01790487 Merc 280 19.2 167.6 -1.09979261 Ferrari Dino 19.7 145.0 -1.24732999 Merc 280C 17.8 167.6 -1.57258064
Additional Resources
How to Perform Simple Linear Regression in R
How to Perform Multiple Linear Regression in R
How to Create a Residual Plot in R