A set is a collection of items.
We denote a set using a capital letter and we define the items within the set using curly brackets. For example, suppose we have some set called “A” with elements 1, 2, 3. We would write this as:
A = {1, 2, 3}
This tutorial explains the most common set operations used in probability and statistics.
Union
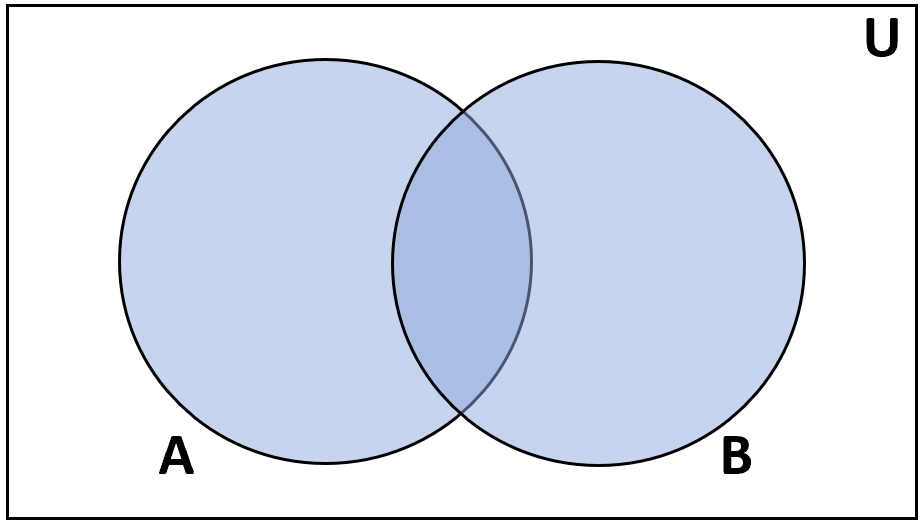
Definition: The union of sets A and B is the set of items that are in either A or B.
Notation: A ∪ B
Examples:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Intersection
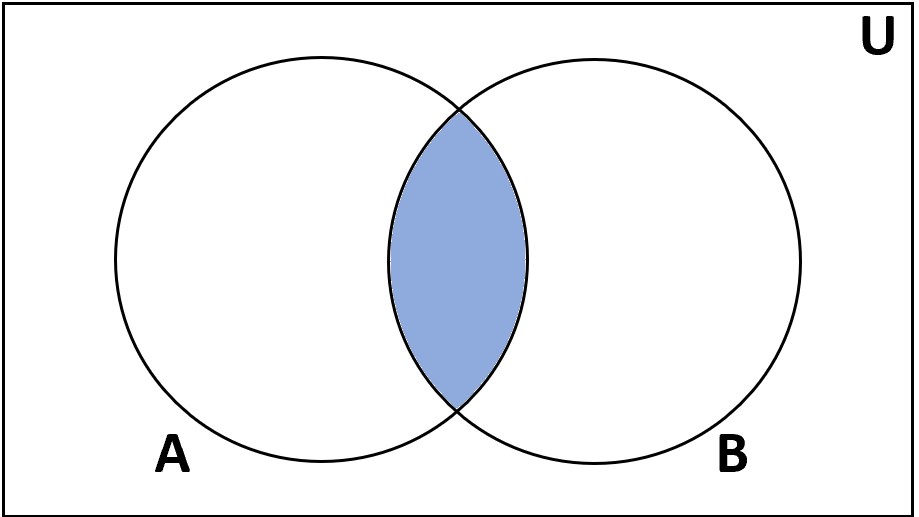
Definition: The intersection of sets A and B is the set of items that are in both A and B.
Notation: A ∩ B
Examples:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Complement
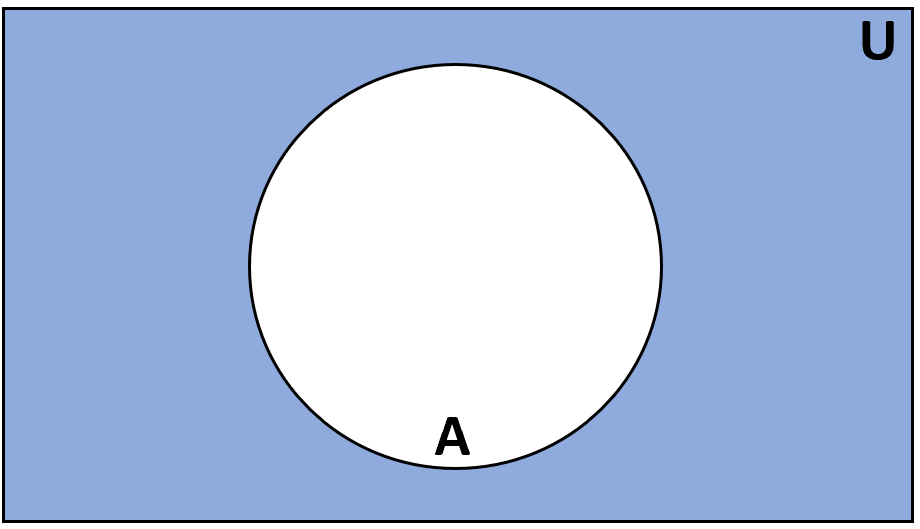
Definition: The complement of set A is the set of items that are in the universal set U but are not in A.
Notation: A’ or Ac
Examples:
- If U = {1, 2, 3, 4, 5, 6} and A = {1, 2}, then Ac = {3, 4, 5, 6}
- If U = {1, 2, 3} and A = {1, 2}, then Ac = {3}
Difference
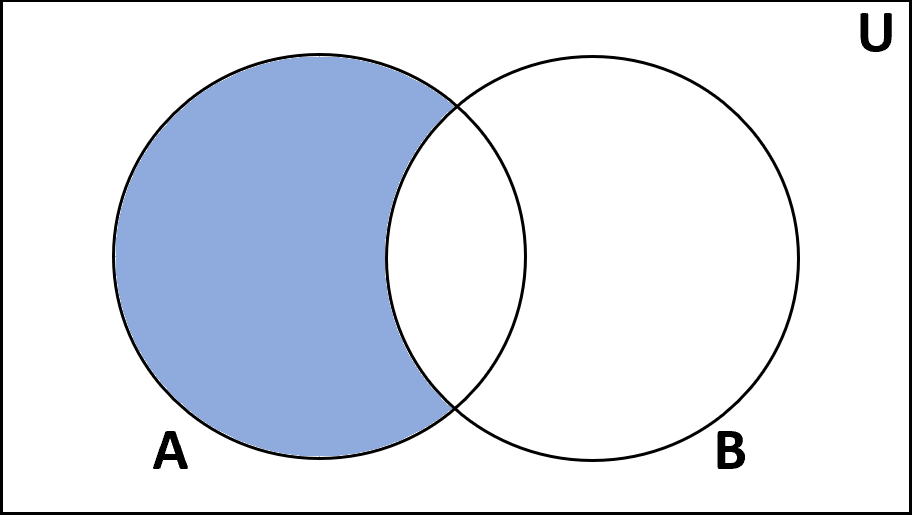
Definition: The difference of sets A and B is the set of items that are in A but not B.
Notation: A – B
Examples:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
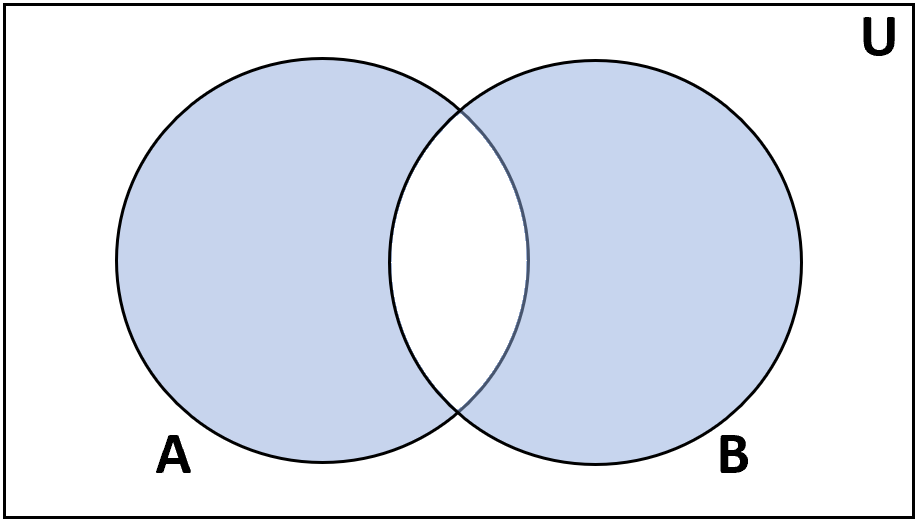
Symmetric Difference
Definition: The symmetric difference of sets A and B is the set of items that are in either A or B, but not in both.
Notation: A Δ B
Examples:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
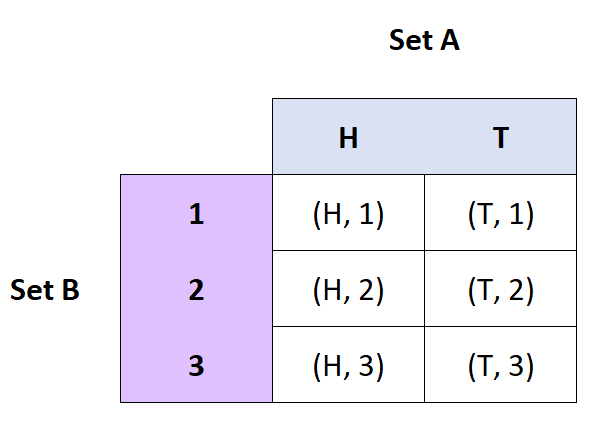
Cartesian Product
Definition: The cartesian product of sets A and B is the set of ordered pairs from A and B.
Notation: A x B
Examples:
- If A = {H, T} and B = {1, 2, 3}, then A x B = {(H, 1), (H, 2), (H, 3), (T, 1), (T, 2), (T, 3)}
- If A = {T, H} and B = {1, 2, 3}, then A x B = {(T, 1), (T, 2), (T, 3), (H, 1), (H, 2), (H, 3)}