In statistics, simple linear regression is a technique we can use to quantify the relationship between a predictor variable, x, and a response variable, y.
When we conduct a simple linear regression, we obtain a “line of best fit” that describes the relationship between x and y, which can be written as:
ŷ = b0 + b1x
where:
- ŷ is the predicted value of the response variable
- b0 is the y-intercept
- b1 is the regression coefficient
- x is the value of the predictor variable
Sometimes we’re interested in using this line of best fit to construct a prediction interval for a given value of x0, which is an interval around the predicted value ŷ0 such that there is a 95% probability that the real value of y in the population corresponding to x0 is within this interval.
The formula to calculate the prediction interval for a given value x0 is written as:
ŷ0 +/- tα/2,df=n-2 * s.e.
where:
s.e. = Syx√(1 + 1/n + (x0 – x)2/SSx)
The formula might look a bit intimidating, but it’s actually straightforward to calculate in Excel. Next, we’ll walk through an example of how to use this formula to calculate a prediction interval for a given value in Excel.
Example: How to Construct a Prediction Interval in Excel
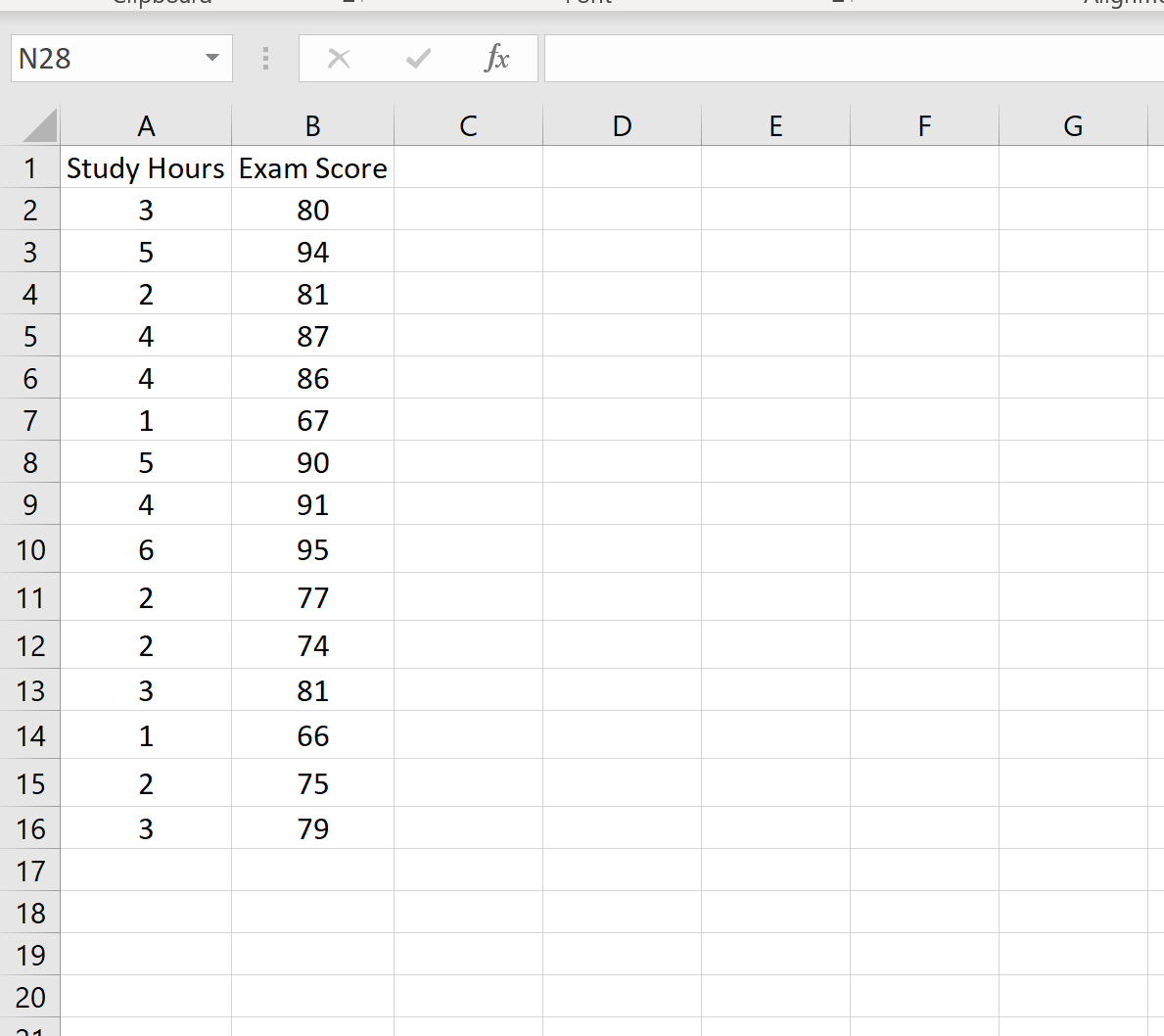
The following dataset shows the number of hours studied along with the exam score received by 15 different students:
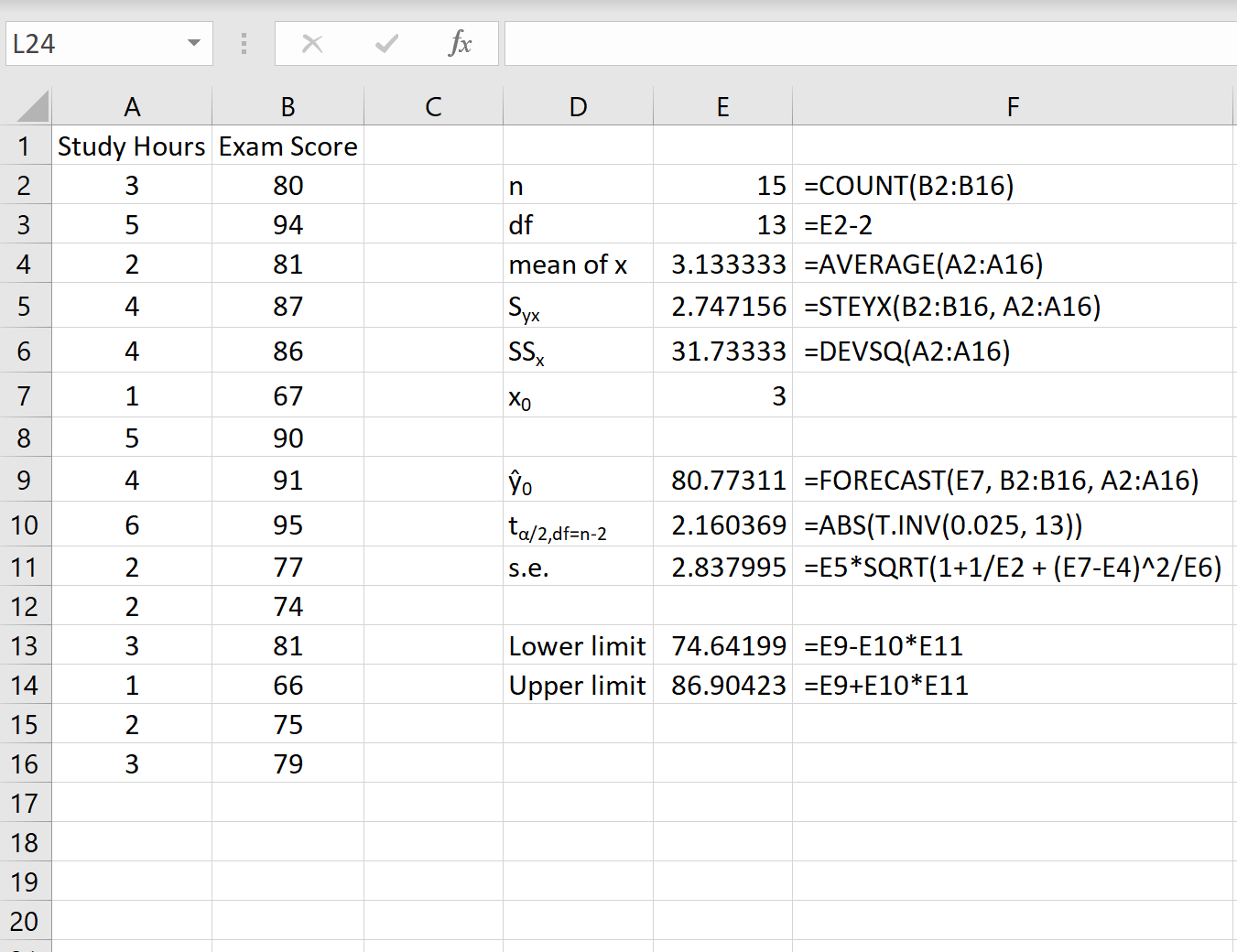
Suppose we would like to create a 95% prediction interval for the value x0 = 3. That is, we want to create an interval such that there is a 95% probability that the exam score is within this interval for a student who studies for 3 hours.
The following screenshot shows how to calculate all of the necessary values to obtain this prediction interval.
Note: The formulas in column F show how the values in column E were calculated.
The 95% prediction interval for a value of x0 = 3 is (74.64, 86.90). That is, we predict with 95% probability that a student who studies for 3 hours will earn a score between 74.64 and 86.90.
A couple notes on the calculations used:
- To calculate the t-critical value of tα/2,df=n-2 we used α/2 = .05/2 = 0.25 since we wanted a 95% prediction interval. Note that higher prediction intervals (e.g. 99% prediction interval) will lead to wider intervals. Conversely, a lower prediction interval (e.g. 90% prediction interval) will lead to a more narrow interval.
- We used the formula =FORECAST() to obtain the predicted value for ŷ0 but the formula =FORECAST.LINEAR() will return the exact same value.